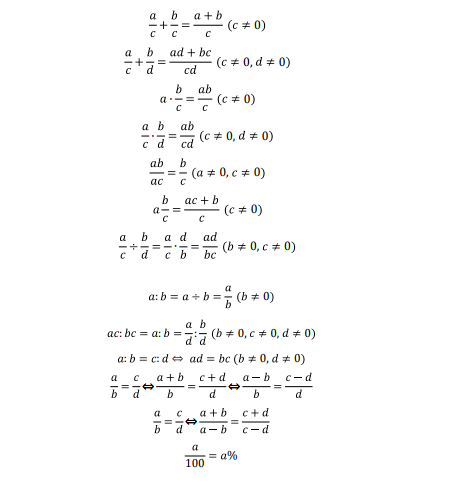在当下教育竞争日益激烈的环境中许多家长都在寻找能够为孩子未来发展加分的途径。其中,AMC8数学竞赛便成为了一个备受瞩目的选择。尽管AMC8被定位为入门级数学竞赛,但它仍然具有一定的挑战性。
一、AMC8竞赛难度特点
1.覆盖范围广
AMC8涵盖了代数运算、几何推理、数论基础、组合数学等八大知识模块。这些内容不仅包括小学阶段的数学知识,还涉及部分初中知识点。
举例:
数论中的最大公约数(GCD)和最小公倍数(LCM)问题,通常需要结合实际情境建立数学模型。
2.逻辑推理能力
约60%的题目需要多步逻辑推理才能解答,这对学生的思维能力提出了较高要求。
举例:
通过构造方程来解决几何问题,或利用排列组合优化解题路径。
题目常设置认知陷阱,例如隐藏的关键条件或文字游戏,需要学生仔细审题并识别关键信息。
模式识别:典型试题往往需要学生快速识别题目类型,并匹配相应的解题方法。
3.时间压力大
时间分配:考试时间为40分钟,共25道题,平均每题仅有96秒(1分36秒)。这不仅考察解题速度,还要求学生具备高效的时间管理能力。
二、AMC8竞赛答题技巧
AMC8竞赛的考试时间仅为40分钟,考生需要在有限的时间内完成25道题目。因此,除了扎实掌握数学知识点外,还需要掌握一些高效的答题技巧,以提升解题速度和准确性。以下是几种常用的答题技巧:
1.特定值法
适用场景:当题目中的条件不够明确或变量较多时,可以通过假设特定值来简化问题。
几何图形问题:
如果几何图形不是唯一确定的,可以假设某些特殊条件(如直角、等边三角形等)进行计算。
比例、百分比、比率问题:
当题目中没有给出总数且总数不影响答案时,可以假设一个方便计算的总数(如100、10等)。
2.度量法
适用场景:适用于几何题,尤其是当图形具备一定对称性或条件较为明确时。
标准图绘制:
如果题目条件能够唯一确定图形,可以画出标准图,并通过测量边长或角度直接得到近似答案。
特殊情况下的图形:
如果题目条件无法唯一确定图形,可以选择一种特殊情况(如正方形、等边三角形等)进行分析和计算。
注意:近年来,AMC8出题人有意规避这种方法,因此度量法的应用机会可能较少,但仍可在简单题中尝试。
3.找规律
适用场景:适用于数列问题、余数求解问题以及涉及周期性的题目。
数列问题:
从最简单的初始情况入手,逐步推导并寻找规律。
余数问题:
余数通常呈现周期性变化,可以通过列举小范围内的例子找到循环规律。
4.排除法
适用场景:适用于选项较多且有一定限制条件的选择题。
奇偶性判断:
根据题目条件,判断答案的奇偶性,排除不符合条件的选项。
取值范围判断:
分析所求问题的可能范围,排除超出范围的选项。
逻辑推理:
对于逻辑推理题,逐一验证每个选项是否符合题意,排除矛盾的选项。
5.时间管理与优先级
快速审题:
在读题时迅速抓住关键信息,避免被文字陷阱误导。
优先解决简单题:
AMC8题目难度由浅入深,前10题通常较简单,建议快速准确完成,为后续难题争取更多时间。
合理放弃:
若遇到特别复杂的题目,可以暂时跳过,优先完成有把握的题目,最后再回头处理。
不知道孩子数学水平如何?
扫码进行AMC8能力测评,看看孩子是否适合参加AMC8!