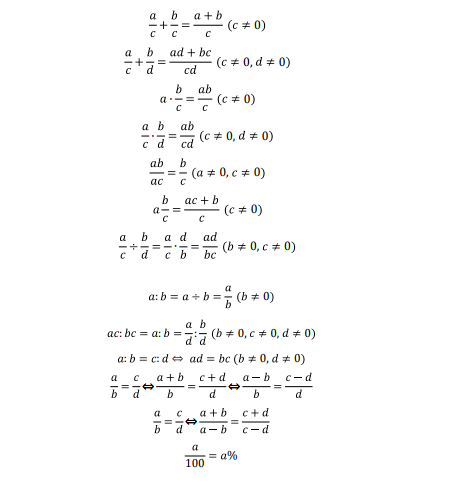AMC8竞赛重难点深度解析！如何用真题高效备考？

AMC8作为全球最具影响力的初中前数学竞赛，虽面向8年级及以下学生，但其知识综合性、思维灵活性和时间压迫感远超普通校内考试。要想在25道题、40分钟内脱颖而出，必须精准把握四大模块的高频考点、核心难点与突破路径。本文结合近年真题趋势，为你系统拆解AMC8的“攻防要点”。

一、AMC8四大模块重难点全景图

模块	高频考点	核心难点	冲刺建议
代数（35%–45%，约10题）	• 分数/小数混合运算 • 比例与百分比应用（折扣、浓度） • 简单方程建模（行程、年龄） • 数列规律（等差、斐波那契）	• 单位换算陷阱（英里↔公里） • 应用题中“隐含等量关系”识别 • 多步计算中的小数点对齐	前15题主力，务必全对！强化“设未知数→列方程→验算”流程
几何（20%–30%，约8题）	• 三角形/四边形面积（割补法） • 勾股定理（含毕达哥拉斯三元组） • 立体图形展开图与染色问题 • 不规则图形面积估算	• 空间想象能力不足（如立方体切分） • 辅助线构造无从下手 • 混淆周长与面积概念	熟记“等积变形+对称性”技巧训练“看图说话”能力，快速提取数量关系
数论（15%–20%，约5题）	• 奇偶性分析 • 整除特征（2,3,4,5,9,11） • GCD/LCM应用 • 同余与余数问题（如“除3余2，除5余3”）	• 对“最小公倍数”实际意义理解模糊 • 余数问题分类讨论不全 • 忽略“正整数”隐含条件	近年比重上升！掌握“枚举+排除”双保险策略
组合（10%–15%，约3–5题）	• 加法/乘法原理 • 路径计数（网格走法） • 韦恩图与容斥原理 • 逻辑推理与分类讨论	• 计数重复或遗漏 • “至少/至多”类问题边界不清 • 缺乏系统分类框架	压轴题常客！目标前1%者必须攻克此模块

趋势洞察：

组合与数论融合题增多（如“满足某同余条件的三位数个数”）；

立体几何+染色问题成新热点（2024年考了立方体表面染色）；

应用题情境更生活化（如游戏规则、投票统计、地图比例尺）。

二、如何用真题高效备考？三大核心策略

策略一：借真题精准定位薄弱模块

操作步骤：

限时模考：选近3年真题（如2022–2024），严格 40分钟独立完成，禁用计算器；

错因深挖：不只看“做错”，更要问：

几何题：是否因不会作辅助线？

数论题：是否混淆了“倍数”与“因数”？

应用题：是否漏读关键条件（如“非负整数”）？

模块归因：按四大模块统计错题占比：

≥30% → 薄弱模块；

≥40% → 需先回归基础（如重新学习勾股定理证明）。

策略二：拆真题突破高频考点

AMC8考点高度重复！近10年数据显示：

“比例应用”出现 68次

“勾股定理”出现 62次

“整除特征”出现 57次

高效做法：

建立专题题库：将2015–2024年真题按考点分类（如“所有比例题”）；

提炼通法：例如“割补法”通用步骤：

步骤1：识别不规则图形可分割为哪些规则图形；

步骤2：计算各部分面积；

步骤3：加总或相减。

形成条件反射：看到“阴影面积”→立刻想“割补/等积/对称”。

策略三：用真题强化应试能力

考前1–2个月，进入全真模拟阶段：

时间分配黄金法则：

题号	目标时间	策略
1–10题	≤15分钟	快速过，确保全对（这是拿奖底线！）
11–20题	≤20分钟	中档题，每题≤2分钟，卡壳即跳
21–25题	≤5分钟	攻坚+检查，不会就空，保底1.5分