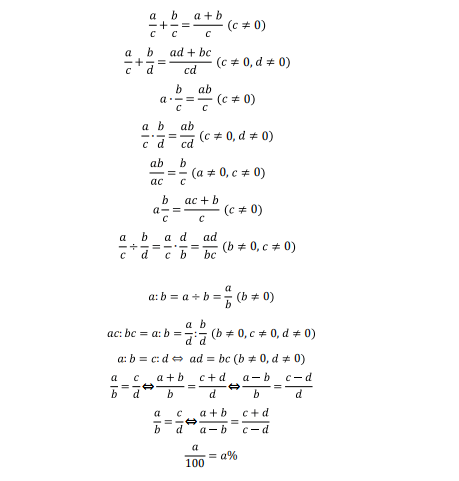AMC8(American Mathematics Competition 8)是美国数学协会(MAA)主办的一项面向全球8年级及以下学生的数学竞赛。它旨在通过挑战性的问题激发学生对数学的兴趣,同时为他们提供展示自己数学能力的机会。
2026年AMC8答案解析

2026年AMC8真题试卷,答案解析、讲解视频、分数线预测等
将在考试静默期结束后第一时间发布!
扫码预约领取⇓

2026 AMC8 考试安排
| 时间节点 | 具体日期 | 备注 |
| 报名截止 | 2026年1月13日 | 确保在此日期前完成报名并获取准考证信息 |
| 考试时间 | 2026年1月23日 17:00-17:40 (中国赛区) | 请提前做好准备,迟到超过15分钟无法进入考场 |
参赛资格
年龄要求:8年级及以下,年龄不超过14.5周岁(无国籍限制)
考试时长:40分钟
题型与分值
25道单选题
答对1题得1分,不答或答错不扣分
满分25分
考试形式
线上/线下:具体由考点安排,提供中英双语试卷
允许携带物品:
黑色/蓝色签字笔
2B铅笔和橡皮
空白草稿纸
符合规定的身份证件
纸质印刷版的英汉字典
禁止使用计算器,通讯设备必须关机
2026 AMC8 高频考点预测
代数(30%-35%)
核心考点:
方程与不等式(含绝对值、二次方程)、函数与图像(一次/二次函数的性质与应用)、数列(等差/等比数列求和与通项)
新趋势:
结合实际问题的代数建模(如“利润最大化”、“行程问题”),需要快速从文字中提炼数学关系。
几何(25%-30%)
核心考点:
圆(圆周角、切线、扇形面积)、三角形(全等/相似、勾股定理应用)、四边形(矩形/菱形/梯形的性质与面积)
新趋势:
几何与代数结合(如坐标系中的图形变换),或涉及3D图形的展开与表面积计算。
数论(10%-15%)
核心考点:
因数分解(质因数、最大公因数/最小公倍数)、同余问题(余数性质)、位值原理(数字谜题)
新趋势:
数论与组合结合(如“数字排列中的奇偶性判断”),需要灵活运用数论性质简化计算。
组合数学(15%-20%)
核心考点:
计数原理(加法/乘法原理)、排列组合(含限制条件的排列)、概率(古典概型与几何概型)
新趋势:
组合问题与几何/数论交叉(如“网格路径计数”、“棋盘染色问题”),需要画图或列表辅助分析。
AMC8 前1%难点解析:攻克最后5题
几何难点:三维立体与复杂组合图形
高频难点:三维展开图动态分析、立体图形截面、勾股定理与实际场景结合(如建筑结构)
破解关键:
熟练掌握特殊三角形(30-60-90、45-45-90)边长比例;
多练习“空间转平面”思维,借助辅助线拆分复杂图形。
组合难点:容斥原理与高阶计数
易错点:多集合交并关系计算时重复计数,或分类标准混乱。
破解关键:
画树状图、列表格梳理逻辑;
复杂问题先简化模型,再逐步拓展,每一步验证是否“互斥且完备”。
数论难点:质因数分解与位值原理结合
近年难度上升:常结合数字谜、极值构造考查。
破解关键:
先分解质因数,再结合位值原理拆分数字;
牢记“质数是数论的基石”,遇到未知数字优先假设为质数验证。
考前建议
1.模考演练
在正式考试前务必完成至少一次完整的在线模考,确保系统兼容性和网络稳定。
使用官方提供的真题进行模拟测试,熟悉题型和答题节奏。
2.知识点梳理
构建知识框架,将代数、几何、数论、组合四大模块的核心考点逐一列出,并标注重点难点。
针对每个模块的高频考点进行专项练习,尤其是最后5道压轴题的类型。
3.答题技巧
时间分配:前20题基础题控制在30分钟内完成,确保准确率;后5题难题留10分钟思考解答。
审题精准:仔细阅读题目,避免因粗心大意而失分。
4.心理准备
提前熟悉考试流程,保持良好的心态和专注力。
合理休息,考试前一天保证充足睡眠,避免熬夜复习。