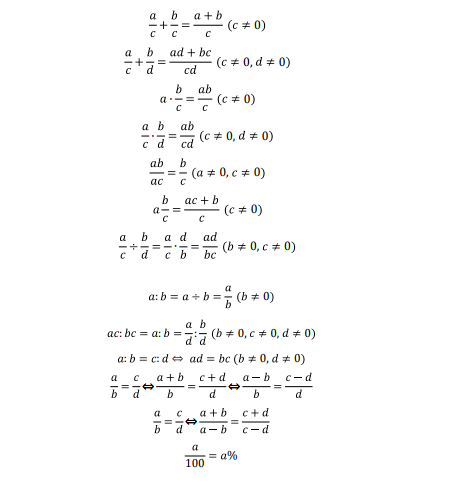AMC8竞赛非常适合8年级以下的低龄学生群体,无论是出于升学、择校还是个人能力提升的目的。以下是从报名需求和考试能力两方面对适合报考AMC8竞赛的学生群体的详细分析:
一、报名需求角度
- 想要获得权威竞赛证书的学生:
对于那些因为各种原因无法顺利拿下奥数比赛,但又需要一份权威竞赛证书来证明自身实力的学生,AMC8是一个不错的选择。
- 计划未来出国读初高中的学生:
目前就读于体制内学校,但有意向在未来出国深造的学生,可以通过参加AMC8来展示自己的数学能力,为留学申请增添一份有力的证明。
- 就读于国际学校的学生:
对于正在国际学校就读,并计划在未来攻读高阶国际课程(如AP等)的学生,AMC8成绩可以作为他们数学能力的一个重要参考。
- 梦想申请美本顶尖院校的学生:
对于那些志在申请藤校等顶尖美本院校的学生,AMC8竞赛成绩无疑能为他们的申请增添一抹亮色。
- 目前在初中就读,希望升入美高的学生:
这些学生可以通过参加AMC8来展示自己的数学实力,为将来升入美国高中打下坚实基础。
- 想要依靠AMC8成绩小升初择校的学生:
在国内,一些优质的初中会考虑学生的AMC8成绩作为入学的一个参考因素,因此参加AMC8对这些学生来说具有择校的意义。
- 想要考入上海三公或进入国际学校的学生:
在上海地区,AMC8成绩被上海三公学校所认可,同时也是进入某些国际学校的重要条件之一。
二、考试能力角度
- 对数学感兴趣的学生:
对于那些真正热爱数学,希望锻炼和提升自己数学思维能力的学生,参加AMC8竞赛无疑是一个很好的选择。
- 已具备四年级数学知识水平的学生:
如果学生已经具备了四年级的数学知识水平,并且在校内数学学习跟得上,不排斥数学学习,那么他们完全有能力参加AMC8竞赛并从中受益。
无论你是出于何种目的,只要你符合上述条件,都不妨尝试一下参加AMC8竞赛吧!
2024年AMC8火热报名中,扫码领取报名表!

扫码免费领取AMC8历年中英真题+备考教材+AMC8必备公式表!