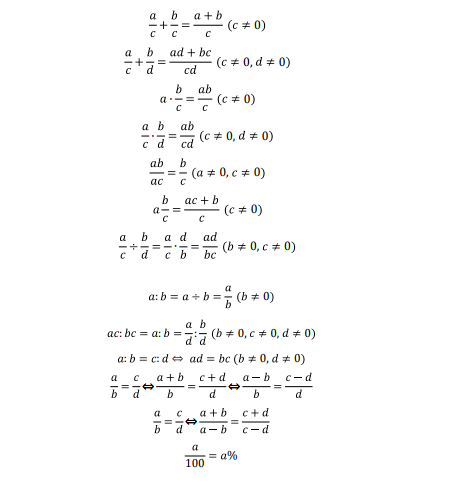对于体制内(国内教育体系)学生,AMC8比赛是小升初的重磅加分项。那么AMC8为何越来越受欢迎?在北上广地区,AMC8有什么用?中国学生备考AMC8有哪些难点?
AMC8为何越来越受欢迎?
最近几年的考试数据显示,2023年AMC8数学竞赛的参赛人数高达7万多人,其中4-6年级学生占参赛人数的26%。随着AMC竞赛影响力的不断扩大,AMC8的低龄段参赛人数也在逐渐增加。
北京AMC8竞赛考情
在北京,AMC8竞赛已成为各大中小学的常规竞赛。知名学府如清华附中、人大附中、首师附中、北大附中等学校都会组织学生参与该竞赛。
上海AMC8竞赛考情
在上海,一些国际学校如包玉刚国际学校、平和双语学校、位育国际学校等也广泛使用AMC8历届真题进行招生考核。
对于上海三公,要求AMC8成绩分别要达到不同的标准:上实需要20分以上,小托福850分以上;浦外需要20分以上,小托福800-850分;上外需要21分以上,小托福850分以上。可见,AMC8的高分对于进入名校至关重要。
中国学生备考AMC8有哪些难点?
1.知识点的全面消化:学生需要确保对所有知识点进行深入理解和消化,因为AMC考察的内容广泛而深入。
2.大量记忆:学生需要记忆更多的常规量、基本题型和理论定理的推导,这需要耗费大量时间和精力。
3.思维应用:学生需要更熟练地运用各种思维方法,面对不同类型的题目能够迅速找到解题思路。
4.解题路径选择:选择解决问题的路径至关重要,一旦选错了方法,问题的解决会变得非常繁琐。
5.快速判断:学生需要通过快速判断,选定计算量最少的解题方式,这需要考验学生的逻辑推理能力和解题速度。
国内学生的数学水平普遍较好,竞争优势较为明显,但是由于美国学生从小学就开始准备AMC8了,所以计划在AMC8竞赛中拿奖的同学,起码要提前半年开始准备!
AMC8数学竞赛暑期班课开启,扫码咨询课程详情!
扫码免费领取AMC8历年中英真题+备考教材+AMC8必备公式表!