AMC10作为美国数学竞赛体系中的重要一环,不仅是对学生数学能力的全面检验,更是通往顶尖大学的关键一步。本文将详细解析 AMC10获奖后的三大核心价值,并提供 科学的备考步骤与课程班型建议,帮助学生在竞赛中脱颖而出。
一、AMC10奖项的三大核心价值
1.学术实力的有力证明
全球卓越奖(Distinguished Honor Roll, 前1%) 和 全球优秀奖(Honor Roll, 前5%) 是国际公认的数学能力标尺。
这些奖项不仅限于数学领域,其考察的能力如逻辑思维、问题解决等对 物理、计算机科学、经济学 等学科的学习同样有直接帮助。
跨学科应用:AMC10培养的数理思维和解题能力是未来学习和研究的基础。
2.世界名校的“敲门砖”
MIT、耶鲁、加州理工 等顶尖大学在申请表中明确要求填写 AMC10/12及AIME成绩。
斯坦福、麻省理工 等名校不仅关注AMC成绩,还会主动联系成绩优异的学生,将其纳入优先录取名单。
3.个人能力的长远提升
注重应用而非死记硬背:AMC10侧重于数学知识的应用,能够有效激发学生的数学兴趣,培养数理思维。
灵活多变的题目设计:与国内数学竞赛的“应试套路”不同,AMC10更注重培养学生的数学思维能力,要求学生在有限时间内快速识别问题本质并选择最优解法。
职场与生活中的宝贵技能:这种能力不仅在学术领域有用,在未来职场和生活中同样宝贵。
二、AMC10备考步骤详解
Step 1: 了解考试内容
知识点覆盖:
小学知识为基础,初中知识为重点,高中知识为难点;
课内“普及”占50%,竞赛“拔高”占50%;
巧妙的思维与基础计算能力的良好结合;
经典竞赛分类AGNC——代数、几何、数论、组合。每个模块考什么,是考前需要认真梳理的!
Step 2: 自我评估
模拟测试:
使用往年真题(建议选2018年以前的题)进行模拟测试;
分代数、几何、数论、组合4个模块评估自己的能力;
根据模测评估自己的计算能力是否为薄弱项。
Step 3: 对症下药
根据评估结果制定策略:
如果已经9年级且距离晋级线差35分以上,建议降低拿奖预期,打好基础;
新手AMC10备考:首先扎实学习代数、几何、数论和组合中的重难点;
晋级AIME的备考方法:按部就班进行真题模拟训练,补充实力打基础。
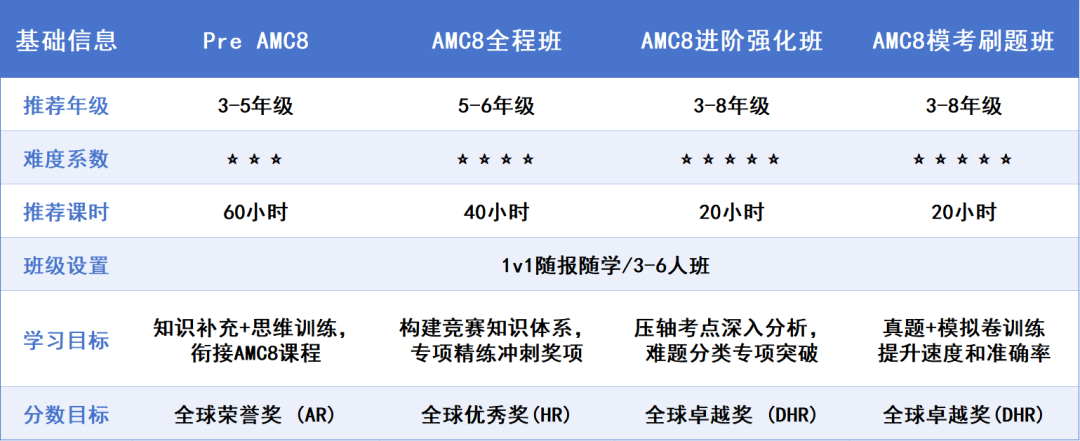
三、AMC10课程班型推荐
1.Pre-AMC10培训课程
适合对象:7~8年级同学,参加AMC8考试取得19分以上的成绩;
目标:为AMC10打下坚实基础,逐步过渡到更高难度的竞赛。
2.AMC10培训课程全程班
适合对象:基础比较差的8~9年级学生;
目标:通过长线备考全面提升数学思维和能力,夯实基础知识。
3.AMC10培训课程优享班
适合对象:基础适中的8~9年级学生;
目标:AMC10基础知识梳理+刷题提高答题速度和正确率。
4.AMC10培训课程基础/强化/冲刺班
适合对象:基础比较好的8~9年级学生,入学前通过测试,精准匹配班型;
目标:根据不同阶段的需求,针对性地进行基础知识巩固、难题攻克和真题模拟训练。
扫码进入AMC10专属学习社群,海量备赛资料&体验课程等你开启!
不知道是否适合AMC10?
扫码回复【在读年级+AMC10测试题】进行AMC10前测题/专业分析评估



扫码【免费领取】AMC10&12历年真题+高频词汇+必备公式⇓