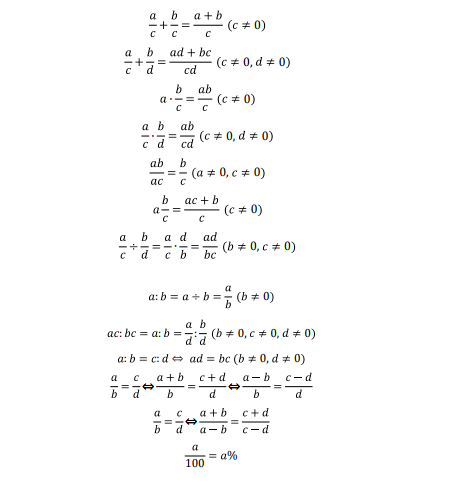随着国际化教育的不断发展,越来越多的学生和家长选择国际学校作为教育的途径。其中,美国AMC数学竞赛作为国际数学竞赛的代表,受到了广泛的关注。
针对不同教育体系下的学生备战AMC数学竞赛,可以采取不同的策略和重点。下面是对体制内、IB/A Level以及AP体系学生的具体建议:
体制内学生
有竞赛经验的学生:如果已经参加过国内的初联或高联,那么你们已经有了很好的基础。由于这些竞赛与AMC在知识点上有较高的重合度,但侧重点有所不同,因此需要多做AMC历年的真题,找出自己的薄弱环节,进行针对性训练。同时,要适应AMC的题目风格和答题节奏。
无竞赛经验的学生:这部分学生通常在函数和几何方面有较好的基础,但在数论、统计及复数等板块可能不够深入。建议从基础知识开始补强,特别是数论和组合数学方面的内容,并通过大量练习来提高解题速度和准确率。
IB和A Level体系学生
学过HL的同学:你们的知识点储备较为充足,但由于英国考试系统对于解题步骤要求非常严谨,而AMC则更加注重结果。因此,需要调整答题方式,培养快速选择正确答案的能力。这包括提高对问题的理解速度和简化计算过程的能力。
备考策略:加强限时条件下的练习,提升解题效率。可以通过模拟考试来习惯AMC的考试模式,减少不必要的步骤书写,专注于寻找最快捷的答案路径。
AP体系学生
微积分背景:AP课程侧重于微积分,而AMC不涉及这一部分。因此,需要特别关注AMC考察的重点领域,如数论、计数和组合数学。
计算器依赖性:AP课程允许使用计算器,而AMC不允许。这意味着需要强化手算能力,尤其是基本运算的速度和准确性。
数字敏感性:增加对数字操作的练习,比如心算技巧,以提高数感。可以通过解决大量的实际问题来增强这方面的能力。
学习重点:集中精力学习数论和排列组合的内容,因为这些是AMC中经常出现且AP课程中较少涉及的主题。
综上所述,根据各自教育体系的特点和个人情况制定合理的备考计划是非常重要的。合理安排时间和精力,有针对性地准备,相信每位学生都能在AMC竞赛中取得满意的成绩。
扫码免费领取AMC历年中英真题+备考教材+AMC必备公式表!
试听AMC名师课程,领取专属福利+AMC一对一备考规划!