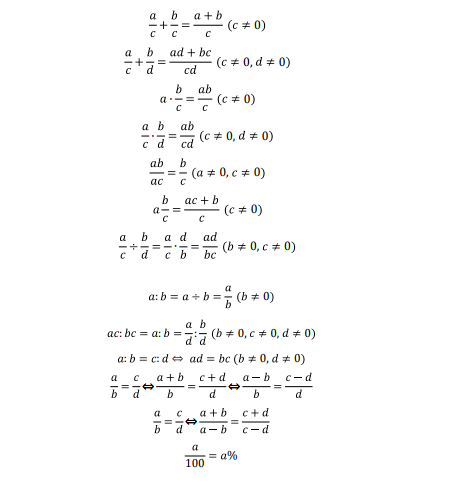AMC8竞赛因其高含金量备受北上广深等城市名校的青睐,特别是在申请国际学校和一些顶尖中学时,AMC8优异的成绩无疑能为学生的申请增添光彩。
2025年AMC8竞赛安排
报名截止时间:2025年1月12日
竞赛时间:2025年1月23日(周四) 10:00-10:40
参赛资格:8年级及以下,且年龄不超过14.5岁
考试语言:中英双语
竞赛时长:40分钟
竞赛题型:25道单项选择题
计分方式:答对一题得1分,答错得0分,满分25分。
考试地点:线上机考/线下考点均可。
考察知识点:不限于分数、百分数、速度、比例等简单运算,简单数论,简单几何(角度,长度与面积计算),简单代数式与方程求解,简单概率与计数、逻辑推理等问题。
奖项设置(个人奖):
—满分奖(Perfect Scores):获得满分25分的同学全球
—卓越奖DHR(Distinguished Honor Roll):全球排名前1%的同学
—全球优秀奖HR(Honor Roll):全球排名前5%的同学
—全球荣誉奖AR(Achievement Roll):六年级及以下且获得15分以上的同学
AMC8竞赛是否需要报班学习?
1.自学能力强的学生
如果您的孩子数学基础较好,自学能力强,且能够自觉地制定学习计划并坚持执行,那么他们可以选择自学AMC8竞赛的相关内容。通过网络资源、教材和参考书籍,他们可以自主学习并提升数学能力。此外,自学还能培养孩子的独立思考和解决问题的能力。(我这里整理了AMC8必备的历年真题和练习题以及公式等,有需要的可以扫码领取哦)
2.数学基础薄弱的学生
对于数学基础薄弱的学生来说,报班学习可能是一个更好的选择。专业的数学老师可以针对孩子的实际情况,制定个性化的教学计划,帮助他们系统地学习AMC8数学知识。此外,老师还可以及时发现并纠正孩子在数学学习中的错误和不足,确保他们能够扎实地掌握每一个知识点。
3.需要系统指导的学生
有些学生虽然数学基础不错,但缺乏系统的竞赛指导和训练。对于这类学生来说,报班学习也是一个不错的选择。专业的竞赛辅导课程通常会涵盖AMC8竞赛的所有知识点,并提供大量的练习题和模拟考试,帮助学生全面提升解题能力和应试技巧。
4.考虑其他因素
除了以上几点外,您还可以考虑以下因素来决定是否报班学习:
时间安排:如果孩子的时间比较紧张,报班学习可以节省他们的时间和精力,因为他们可以在老师的指导下高效地学习。
学习氛围:参加培训班可以让孩子与其他同龄人一起学习,共同进步。这种学习氛围往往能够激发孩子的学习动力和竞争意识。
以上建议仅供各位同学和家长参考,大家合理参考即可。
不知道孩子数学水平如何?
扫码进行AMC8能力测评,看看孩子是否适合参加AMC8!

扫码免费领取AMC8近20年中英真题+备考教材+AMC8必备公式集+词汇表!