AMC8数学竞赛在国际教育界中拥有很高的声望和认可度,参加和突出表现在此竞赛中,无论对于小升初的学生,还是有志于进入国际学校和美国高中的初中生,都具有深远的影响。
AMC8竞赛是针对八年级以下学生开设的竞赛,但根据2022年参赛数据分析,AMC8实际参赛年龄,1-8年级不等,其中:
四年级及以下 : 1105人,占比1.5%;
五年级:3231人,占比4.5%
六年级:14258人,占比20%
七年级: 22493,占比31.6%
八年级:29236人,占比41.2%
AMC8竞赛适合几年级?
对于3年级以下的学生,由于他们的思维习惯和能力可能还未完全成熟,学习AMC8可能会比较困难。因此,一般不建议这个年龄段的学生过早接触AMC8竞赛。学霸型学生可以适当接触学习。
对于4-5年级的学生,他们已经具备了一定的数学基础和学习能力,可以开始着手准备小奥或AMC8竞赛。
到了6年级,学生的数学知识和解题能力应该有了更进一步的提升。此时,他们的AMC8考试目标可以设定为获得17+的分数,争取进入全球排名前5%。对于基础较好的学生,他们可以将目标定得更高,争取进入全球前1%。
7-8年级的学生的数学水平已经相对较高,对AMC8竞赛的掌握应该更加深入。在这个阶段,学生的成绩目标应该是全球排名前1%,分数大约在22分左右。基础好的学生可以考虑提前准备AMC10的知识,并将AMC10的目标定在90+。
AMC8数学竞赛有什么用?
国际学校和本科留学的优势:AMC8竞赛的国际知名度和认可度高,对于对外国大学入学的申请者,尤其是那些有志于冲击世界顶尖大学的学生来说,AMC8成绩无疑可以提供强有力的支持,展示他们的数学才华和潜力。
小升初竞争优势:对于小学生,在小升初这个关键阶段,AMC8的成绩已经成为了一种重要的"硬通货"。一些享有自主招生权的优质初中,比如上海的"三公",非常看重AMC8的成绩,好的成绩可以让学生在竞争中脱颖而出。
提升逻辑思维:与一些高难度的奥数竞赛相比,AMC8的难度适宜,题目多样,更加亲和,因此被更多的学生所接受。同时,参加AMC8竞赛,不仅可以锻炼和提升学生们的逻辑思维能力,对数学的热情和兴趣,还可以提升学生的普通课内成绩,为升学之路增添加分项。
无论是对于个人发展还是升学竞争,AMC8都提供了宝贵的机遇。学生们在参加AMC8竞赛的过程中,可以既得到乐趣,又能在学习中不断收获成长。
扫码免费领取AMC8历年中英真题+备考教材+AMC8必备公式表!

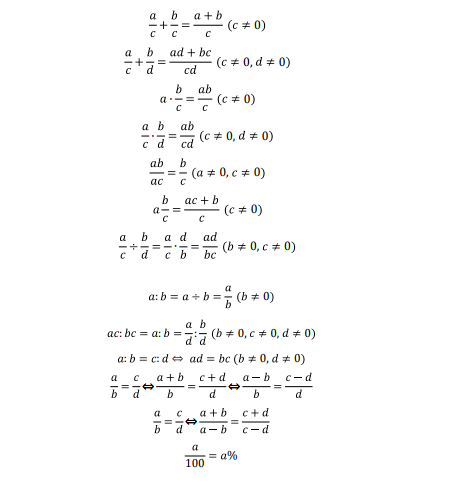
AMC8数学竞赛课程长线班课开启,扫码咨询课程详情!