2023年AMC10/12分数线已经公布!2023年AMC10/12分数线是多少?相较往年AMC10/12分数线更高吗?AMC10/12赛后如何规划?
第一种:继续备战AIME竞赛
适合在AMC10/12竞赛中顺利晋级AIME竞赛的同学。AIME竞赛的难度更高,对学生的数学综合能力要求更高。在AIME竞赛中取得8分以上的成绩对于申请名校更有利。
第二种:长线备考来年的AMC10/12
适合在2023年AMC10/12竞赛中表现不佳的同学。AMC10/12竞赛本身就有一定的难度,没有经过充分准备或数学基础一般的同学很难在激烈的竞争中脱颖而出。即使考试成绩不理想,重要的是吸取经验教训,总结知识盲点,开启AMC10/12竞赛的长线备考,冲刺奖项,并辅助校内数学提升。
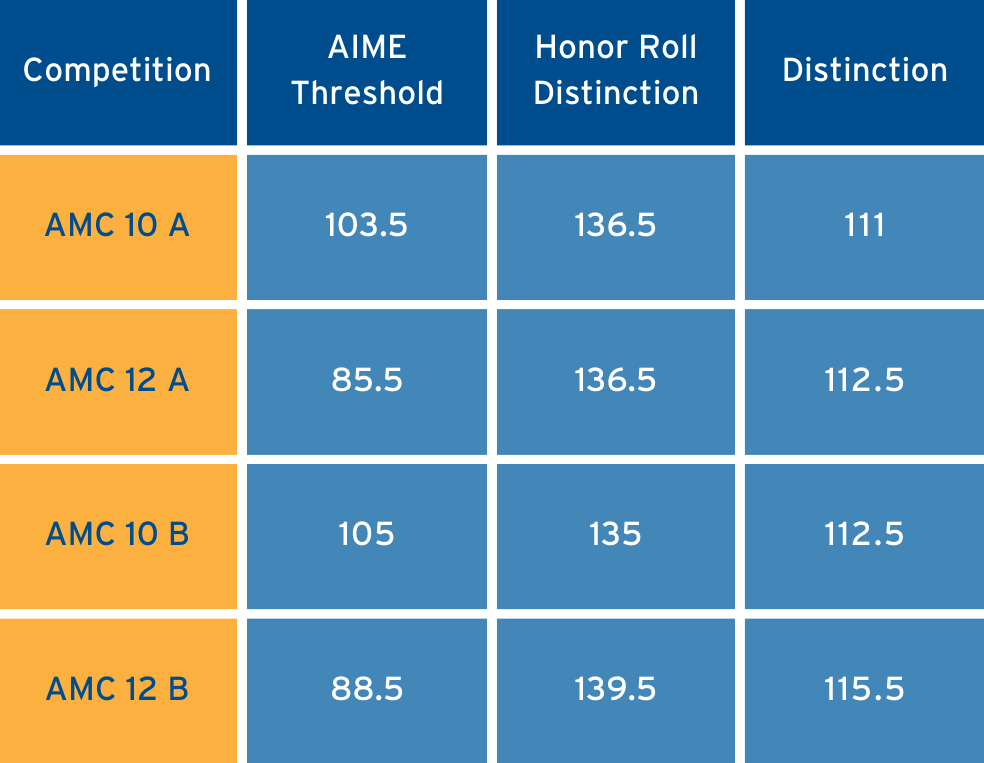
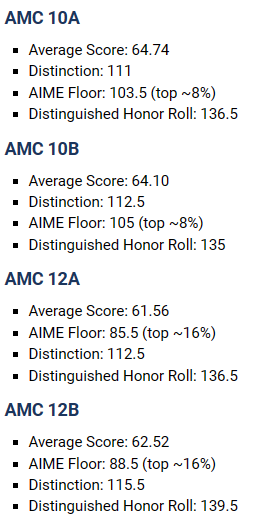
2023年AMC 10/12分数线分析
AMC 10
今年的AMC 10考试相较去年明显降低了难度,特别是B卷的难度也有所下降。大部分学生都是A、B卷双报,第一次考完之后吸取经验教训,通过一周的冲刺,很可能在第二次考试中发挥更稳定一些。因此,A、B卷的AIME、Distinction以及DHR的分数线相差甚小也在情理之中。
AMC 12
此次AMC 12考试,AIME Cutoff有些过低,A卷的85.5分已经接近此前历史的最低值84分。与A卷相比,12B卷在难题部分的考察要求显著降低,这也反映在DHR的分数线较A卷有所升高,已经接近140的极高分。
可能是因为一方面,虽然本次AMC的难度整体相较去年有明显降低,但在整个历史上纵向相比,近年来的赛题从计算量和解题思路的复杂度上都较以前有质的提高。
编号不高的题目中频频出现远比预期更难啃的硬骨头题目,从而导致在非常紧张的时间内完成更多的题目更为困难,也就导致在全球范围的考生中AIME的晋级分数线始终不高。
另一方面,今年12A卷和B卷都出现了函数方程这个作为MO级别比赛常客的非常经典的数学竞赛内容。而在历史的AMC和AIME考题中,这部分题目出现得并不多。
这再次印证了AMC作为目前世界上设置最科学的数学竞赛之一,每一次比赛都会尝试一些在历史上没有考察过或者较少考察过的新的题型和考点。
扫码咨询AIME冲刺课程+免费领取AIME历年真题&答案详解,先到先得!