1990年AJHSME 真题及答案 - American Mathematics Competitions

1990年AJHSME 真题：

Problem 1

What is the smallest sum of two $3$ -digit numbers that can be obtained by placing each of the six digits $4,5,6,7,8,9$ in one of the six boxes in this addition problem?

$[asy] unitsize(12); draw((0,0)--(10,0)); draw((-1.5,1.5)--(-1.5,2.5)); draw((-1,2)--(-2,2)); draw((1,1)--(3,1)--(3,3)--(1,3)--cycle); draw((1,4)--(3,4)--(3,6)--(1,6)--cycle); draw((4,1)--(6,1)--(6,3)--(4,3)--cycle); draw((4,4)--(6,4)--(6,6)--(4,6)--cycle); draw((7,1)--(9,1)--(9,3)--(7,3)--cycle); draw((7,4)--(9,4)--(9,6)--(7,6)--cycle); [/asy]$

$\text{(A)}\ 947 \qquad \text{(B)}\ 1037 \qquad \text{(C)}\ 1047 \qquad \text{(D)}\ 1056 \qquad \text{(E)}\ 1245$

Problem 2

Which digit of $.12345$ , when changed to $9$ , gives the largest number?

$\text{(A)}\ 1 \qquad \text{(B)}\ 2 \qquad \text{(C)}\ 3 \qquad \text{(D)}\ 4 \qquad \text{(E)}\ 5$

Problem 3

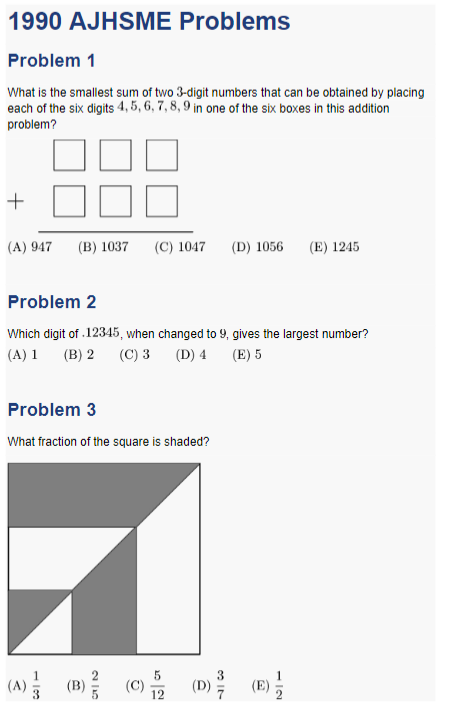
What fraction of the square is shaded?

$[asy] draw((0,0)--(0,3)--(3,3)--(3,0)--cycle); draw((0,2)--(2,2)--(2,0)); draw((0,1)--(1,1)--(1,0)); draw((0,0)--(3,3)); fill((0,0)--(0,1)--(1,1)--cycle,grey); fill((1,0)--(1,1)--(2,2)--(2,0)--cycle,grey); fill((0,2)--(2,2)--(3,3)--(0,3)--cycle,grey); [/asy]$

$\text{(A)}\ \frac{1}{3} \qquad \text{(B)}\ \frac{2}{5} \qquad \text{(C)}\ \frac{5}{12} \qquad \text{(D)}\ \frac{3}{7} \qquad \text{(E)}\ \frac{1}{2}$