1988年AJHSME 真题及答案 - American Mathematics Competitions

1988年AJHSME 真题：

Problem 1

The diagram shows part of a scale of a measuring device. The arrow indicates an approximate reading of

$[asy] draw((-3,0)..(0,3)..(3,0)); draw((-3.5,0)--(-2.5,0)); draw((0,2.5)--(0,3.5)); draw((2.5,0)--(3.5,0)); draw((1.8,1.8)--(2.5,2.5)); draw((-1.8,1.8)--(-2.5,2.5)); draw((0,0)--3*dir(120),EndArrow); label("$10$",(-2.6,0),E); label("$11$",(2.6,0),W); [/asy]$

$\text{(A)}\ 10.05 \qquad \text{(B)}\ 10.15 \qquad \text{(C)}\ 10.25 \qquad \text{(D)}\ 10.3 \qquad \text{(E)}\ 10.6$

Problem 2

The product $8\times .25\times 2\times .125 =$

$\text{(A)}\ \frac18 \qquad \text{(B)}\ \frac14 \qquad \text{(C)}\ \frac12 \qquad \text{(D)}\ 1 \qquad \text{(E)}\ 2$

Problem 3

$\frac{1}{10}+\frac{2}{20}+\frac{3}{30} =$

$\text{(A)}\ .1 \qquad \text{(B)}\ .123 \qquad \text{(C)}\ .2 \qquad \text{(D)}\ .3 \qquad \text{(E)}\ .6$

Problem 4

The figure consists of alternating light and dark squares. The number of dark squares exceeds the number of light squares by

$\text{(A)}\ 7 \qquad \text{(B)}\ 8 \qquad \text{(C)}\ 9 \qquad \text{(D)}\ 10 \qquad \text{(E)}\ 11$

$[asy] unitsize(12); //Force a white background in middle even when transparent fill((3,1)--(12,1)--(12,4)--(3,4)--cycle,white); //Black Squares, Gray Border (blends better than white) for(int a=0; a<7; ++a) { filldraw((2a,0)--(2a+1,0)--(2a+1,1)--(2a,1)--cycle,black,gray); } for(int b=7; b<15; ++b) { filldraw((b,14-b)--(b+1,14-b)--(b+1,15-b)--(b,15-b)--cycle,black,gray); } for(int c=1; c<7; ++c) { filldraw((c,c)--(c+1,c)--(c+1,c+1)--(c,c+1)--cycle,black,gray); } filldraw((6,4)--(7,4)--(7,5)--(6,5)--cycle,black,gray); filldraw((7,5)--(8,5)--(8,6)--(7,6)--cycle,black,gray); filldraw((8,4)--(9,4)--(9,5)--(8,5)--cycle,black,gray); //White Squares, Black Border filldraw((7,4)--(8,4)--(8,5)--(7,5)--cycle,white,black); for(int a=0; a<7; ++a) { filldraw((2a+1,0)--(2a+2,0)--(2a+2,1)--(2a+1,1)--cycle,white,black); } for(int b=9; b<15; ++b) { filldraw((b-1,14-b)--(b,14-b)--(b,15-b)--(b-1,15-b)--cycle,white,black); } for(int c=1; c<7; ++c) { filldraw((c+1,c)--(c+2,c)--(c+2,c+1)--(c+1,c+1)--cycle,white,black); } label("same",(6.3,2.45),N); label("pattern here",(7.5,1.4),N); [/asy]$

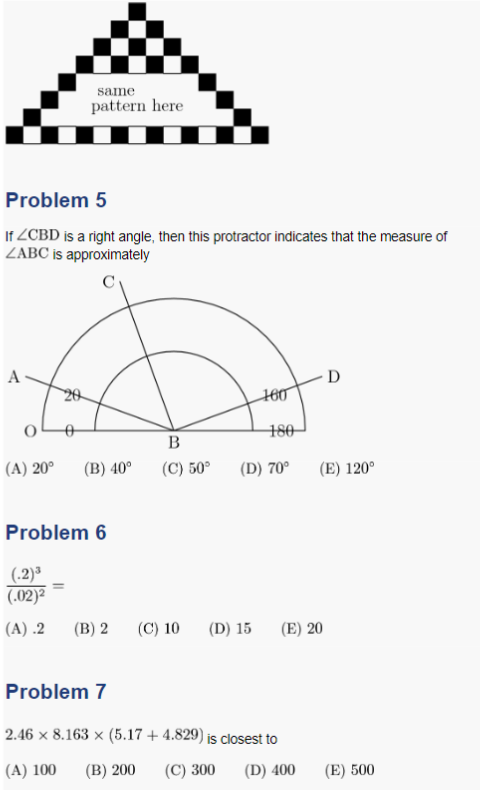
Problem 5

If $\angle \text{CBD}$ is a right angle, then this protractor indicates that the measure of $\angle \text{ABC}$ is approximately

$[asy] unitsize(36); pair A,B,C,D; A=3*dir(160); B=origin; C=3*dir(110); D=3*dir(20); draw((1.5,0)..(0,1.5)..(-1.5,0)); draw((2.5,0)..(0,2.5)..(-2.5,0)--cycle); draw(A--B); draw(C--B); draw(D--B); label("O",(-2.5,0),W); label("A",A,W); label("B",B,S); label("C",C,W); label("D",D,E); label("0",(-1.8,0),W); label("20",(-1.7,.5),NW); label("160",(1.6,.5),NE); label("180",(1.7,0),E); [/asy]$