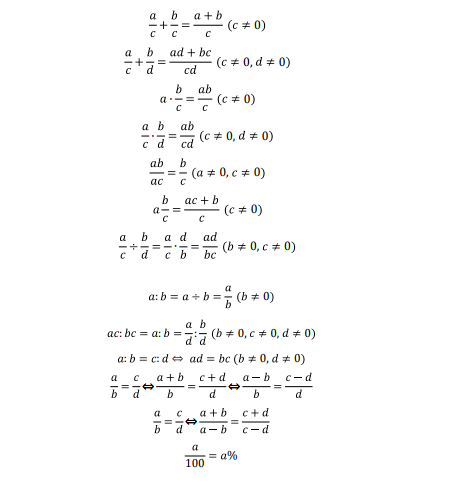AMC8是美国数学协会(MAA)为8年级及以下学生设计的国际数学竞赛,作为AMC系列竞赛的起点,它不仅是检验数学能力的重要标准,更是培养逻辑思维、衔接高阶竞赛(AMC10/12 → AIME)的关键跳板。
一、AMC8 七大高频考点详解
AMC8考试共25道选择题,涵盖小学至初中低年级数学知识,并融合部分校内不涉及的竞赛内容。以下是近年来出现频率最高、得分权重最大的七大模块:
1. 计算部分
| 考点 | 内容说明 | 备考建议 |
|---|---|---|
| 分数/小数/百分数运算 | 加减乘除、四则混合、单位换算 | 熟练掌握通分、约分、小数与分数互化 |
| 估算与近似 | 判断数量级、合理舍入 | 培养数感,避免过度精确计算 |
| 运算技巧 | 提取公因式、分配律、裂项相消 | 掌握简便算法,提升速度 |
特点:难度较低,但易因粗心失分,需注意单位、括号、顺序等细节。
2. 应用题部分
| 考点 | 典型题型 | 解题策略 |
|---|---|---|
| 行程问题 | 相遇、追及、平均速度 | 画图+列方程,设未知数建模 |
| 年龄问题 | 年龄差恒定 | 找不变量,列等式 |
| 工程问题 | 合作效率 | 设总工作量为1 |
| 逻辑推理 | 条件判断、真假话 | 列表法、排除法、假设法 |
关键能力:理解题意、提取信息、建立数学模型
3. 几何部分
| 考点 | 核心内容 | 必备技能 |
|---|---|---|
| 平面图形 | 三角形、矩形、圆、扇形的周长与面积 | 熟记公式,灵活拆分 |
| 不规则图形面积 | 拆分法、割补法、对称法、整体减空白 | 动手画辅助线 |
| 立体几何 | 正方体/长方体展开图、表面积、体积 | 空间想象+动手折纸 |
| 勾股定理 | 直角三角形边长计算 | 掌握常见勾股数组(3-4-5, 5-12-13) |
4. 计数部分
| 考点 | 核心原理 | 常见模型 |
|---|---|---|
| 加法原理 | 分类计数 | “或”关系 |
| 乘法原理 | 分步计数 | “且”关系 |
| 排列组合 | 有序 vs 无序 | 握手问题、路线计数 |
| 容斥原理 | 多集合重叠 | 两集合/三集合文氏图 |
5. 组合数学
涉及初步的逻辑推理,多用列表、画图、枚举辅助思考。
6. 数论部分
涉及较为初步的质数与合数、约数与倍数、整除问题、余数问题,多次考察了位值原理。数论部分中概念比较多、容易混淆,所以在复习的时候首先要弄清楚每部分内容的概念与性质和计算方法。
7. 其他考点(占比约5–10%)
| 考点 | 内容说明 |
|---|---|
| 概率 | 简单事件概率、独立事件 |
| 统计 | 平均数、中位数、众数、极差 |
| 坐标系 | 点的位置、对称点、距离 |
| 图表理解 | 条形图、折线图、饼图数据读取 |
二、AMC8 数学竞赛难度解析
AMC8题目按难度呈梯度上升,适合不同水平的学生逐步挑战:
| 难度层级 | 题号范围 | 考察重点 | 目标正确率 | 备考建议 |
|---|---|---|---|---|
| 基础层 | 1–10 | 课内知识、基本运算、简单应用 | 100% | 确保零失误,注意单位、选项陷阱 |
| 进阶层 | 11–15 | 单一知识点深化(如排列、一次函数) | ≥80% | 专项训练,掌握典型题型 |
| 挑战层 | 16–20 | 跨模块综合(几何+代数、数论+计数) | ≥50% | 提升模型转化能力,学会拆解问题 |
| 高难层 | 21–25 | 多领域融合、创新思维题(压轴题) | 建议主攻1–2题 | 学会策略性放弃,合理猜题 |
三、AMC8 自学还是报班?决策指南
适合自学AMC8的学生:
| 条件 | 说明 |
|---|---|
| 孩子数学拔尖 | 校内数学稳定95+,理解力强,逻辑清晰 |
| 自律性强 | 能主动安排学习计划,坚持刷题总结 |
| 家长可辅导 | 有理工背景,能看懂错题、提炼方法 |
| 目标适中 | 以体验竞赛、拓展思维为主,不强求前1% |
适合报班学习AMC8的学生:
| 条件 | 说明 |
|---|---|
| 缺乏竞赛思维 | 遇到难题“卡壳”,不会转化模型 |
| 自学效率低 | 刷题无方向,错题不分析,容易放弃 |
| 家长无时间/能力辅导 | 工作繁忙或数学基础薄弱 |
| 目标明确 | 冲刺全球前5%或前1%,用于升学背书 |
报班价值:
系统梳理知识点,避免遗漏
老师引导解题思路,突破思维瓶颈
高频考点专项突破,事半功倍
模拟考试+错题精讲,提升应试能力
2026赛季AMC8报名开启!
我们是官方授权线下&线上考点,扫码领取报名表,免费代报名⇓