2012年AIME II 真题及答案 - American Mathematics Competitions

2012年AIME II 真题：

Problem 1

Find the number of ordered pairs of positive integer solutions $(m, n)$ to the equation $20m + 12n = 2012$ .

Problem 2

Two geometric sequences $a_1, a_2, a_3, \ldots$ and $b_1, b_2, b_3, \ldots$ have the same common ratio, with $a_1 = 27$ , $b_1=99$ , and $a_{15}=b_{11}$ . Find $a_9$ .

Problem 3

At a certain university, the division of mathematical sciences consists of the departments of mathematics, statistics, and computer science. There are two male and two female professors in each department. A committee of six professors is to contain three men and three women and must also contain two professors from each of the three departments. Find the number of possible committees that can be formed subject to these requirements.

Problem 4

Ana, Bob, and Cao bike at constant rates of $8.6$ meters per second, $6.2$ meters per second, and $5$ meters per second, respectively. They all begin biking at the same time from the northeast corner of a rectangular field whose longer side runs due west. Ana starts biking along the edge of the field, initially heading west, Bob starts biking along the edge of the field, initially heading south, and Cao bikes in a straight line across the field to a point $D$ on the south edge of the field. Cao arrives at point $D$ at the same time that Ana and Bob arrive at $D$ for the first time. The ratio of the field's length to the field's width to the distance from point $D$ to the southeast corner of the field can be represented as $p : q : r$ , where $p$ , $q$ , and $r$ are positive integers with $p$ and $q$ relatively prime. Find $p+q+r$ .

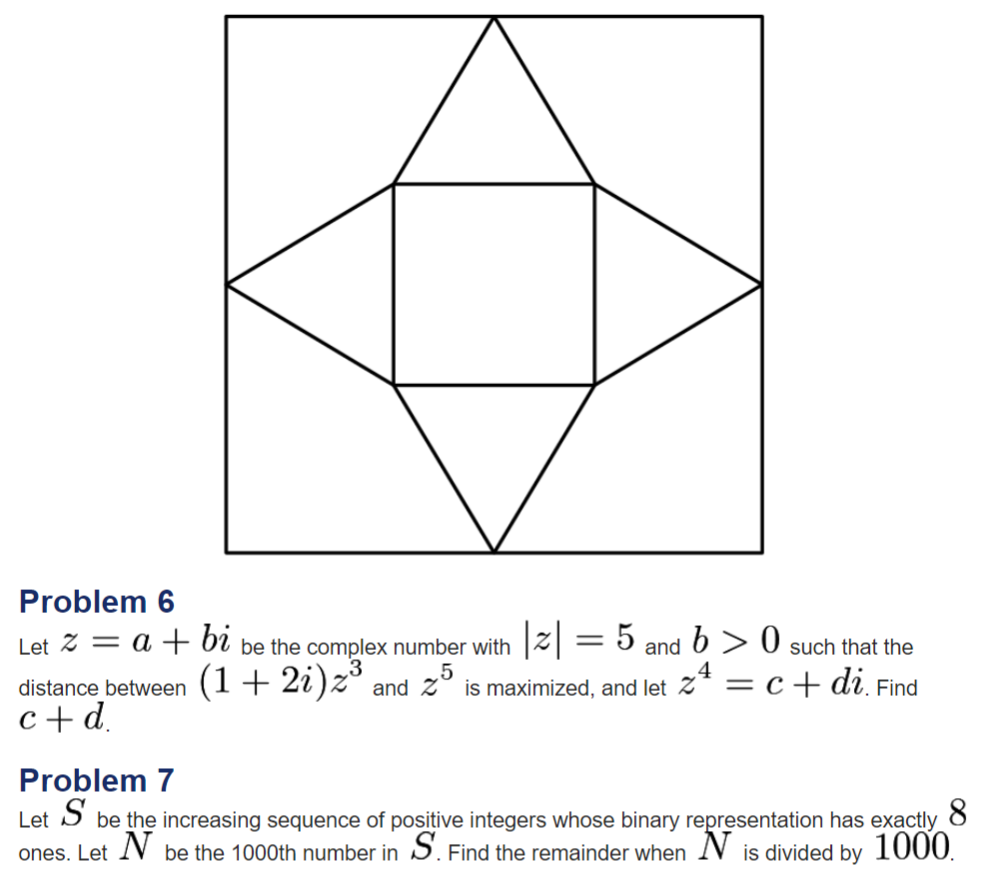
Problem 5

In the accompanying figure, the outer square $S$ has side length $40$ . A second square $S'$ of side length $15$ is constructed inside $S$ with the same center as $S$ and with sides parallel to those of $S$ . From each midpoint of a side of $S$ , segments are drawn to the two closest vertices of $S'$ . The result is a four-pointed starlike figure inscribed in $S$ . The star figure is cut out and then folded to form a pyramid with base $S'$ . Find the volume of this pyramid.

$[asy] pair S1 = (20, 20), S2 = (-20, 20), S3 = (-20, -20), S4 = (20, -20); pair M1 = (S1+S2)/2, M2 = (S2+S3)/2, M3=(S3+S4)/2, M4=(S4+S1)/2; pair Sp1 = (7.5, 7.5), Sp2=(-7.5, 7.5), Sp3 = (-7.5, -7.5), Sp4 = (7.5, -7.5); draw(S1--S2--S3--S4--cycle); draw(Sp1--Sp2--Sp3--Sp4--cycle); draw(Sp1--M1--Sp2--M2--Sp3--M3--Sp4--M4--cycle); [/asy]$ Problem 6

Let $z=a+bi$ be the complex number with $\vert z \vert = 5$ and $b > 0$ such that the distance between $(1+2i)z^3$ and $z^5$ is maximized, and let $z^4 = c+di$ . Find $c+d$ .

以下是我们为您整理的真题试卷，扫码即可免费领取完整版：

更多AIME 历年真题+真题详解
扫码添加顾问即可免费领取