在中国的国际学校中,AMC10和AMC12的竞赛被认为是进入高质量大学的关键通行证。在深国交、贝赛思、鼎石、上海世外等学校,学生们通常会提前报名参加这些数学竞赛。AMC10和AMC12往往是紧密相连的,也有很多家长和同学们感到困惑,AMC10和AMC12有什么异同点?
AMC10与AMC12不同点
AMC10和AMC12是美国数学竞赛系列中两个重要的竞赛,它们在参赛对象、含金量和晋级AIME的标准上有所不同。以下是详细的对比分析:
1.参赛对象区别
AMC10 数学竞赛
参赛对象:主要针对10年级及以下的学生,且要求考试当天学生的年龄不超过17.5岁。
适合年级:适合7-10年级的学生参加,尤其是那些在数学方面有兴趣和潜力的学生。
AMC12 数学竞赛
参赛对象:主要针对12年级及以下的学生,且要求考试当天学生的年龄不超过19.5岁。
适合年级:适合9-12年级的学生参加,特别是那些已经掌握了较高级别数学知识的学生。
2.含金量对比
AMC12难度更高,所考察的数学知识更为广泛和深入,包括高中数学的高级主题。因此,AMC12的含金量要高于AMC10。
3.晋级AIME的标准
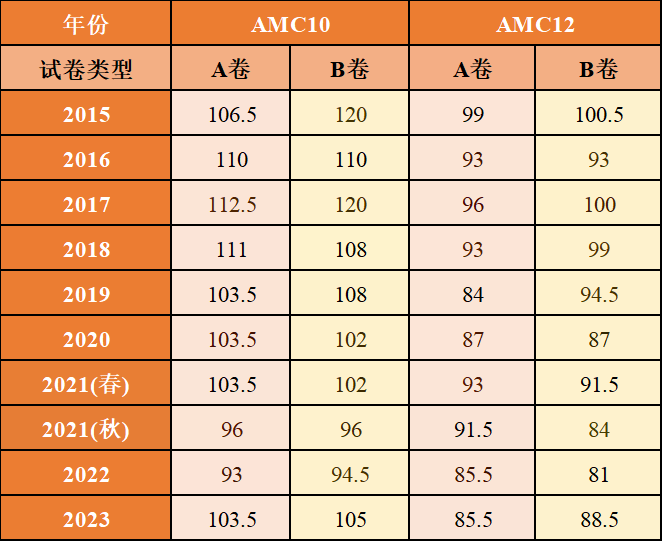
虽然两个竞赛都有机会晋级AIME,但它们的晋级标准有所不同。AMC12晋级AIME的分数线会比AMC10晋级的分数线低20%左右,且AMC12晋级AIME的人数比例会更高一些。
AMC10与AMC12的相同点
1.考试时间
- 两个竞赛都分为A卷和B卷,分别在每年的不同时间段进行。通常情况下,A卷和B卷的考试日期相隔一周左右。
- 考生可以选择参加其中一场或两场考试,根据自身的准备情况和时间安排做出选择。
2.考试形式
- AMC10和AMC12均为个人赛,采用笔试形式。
- 考试时间都是75分钟,考试语言提供中英双语版本,以适应不同背景的考生。
- 题型相同,均为25道选择题(5选1),题目设计上注重考察学生的逻辑思维能力和数学知识的应用能力。
3.评分标准
答对每题得6分,共计150分满分。不作答的题目每题得1.5分,答错不扣分。
注:A卷和B卷是不同试卷,但同等难度和考试范围,同学可以任选A或B卷参加考试,也可以都参加,最终取A卷和B卷的最高个人成绩参与评奖排名和AIME晋级邀请赛。
2024年AMC10/12火热报名中,扫码领取报名表!

扫码【免费领取】历年真题!