我们的AMC辅导课程配有独家自研教材,授课老师均为海内外名校毕业,具有丰富的竞赛教学经验,并根据不同基础学生开设了不同的班课,真正做到有的放矢,事半功倍!
AMC8/10/12/AIME 9.9元试听课 滚动开班!

最新课程安排

扫码试听 了解课程安排⇓


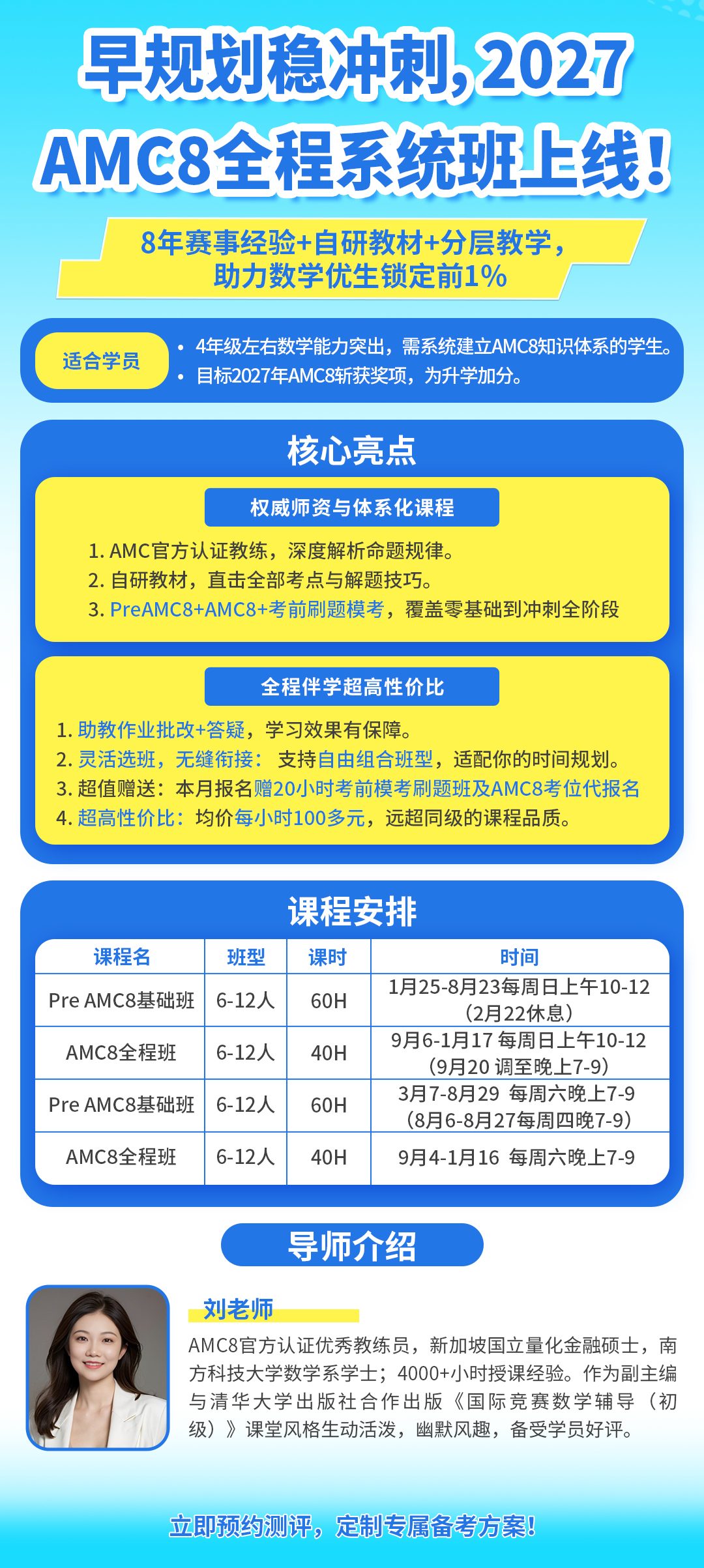
扫码报名课程,了解课程详情⇓

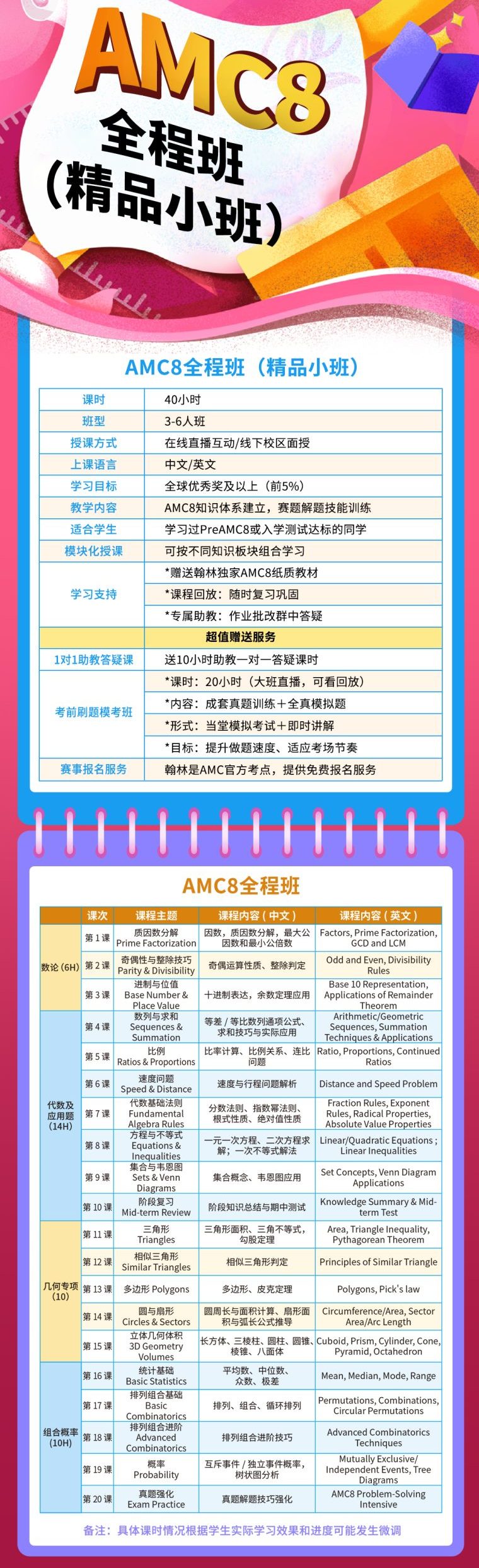


扫码试听 了解课程安排⇓

导师阵容(部分)
Z老师
美国罗切斯特大学理论数学博士
复旦大学上海数学中心博士后研究员
官方认证AMC优秀教练
初中阶段获得全国初中数学联赛一等奖、化学联赛二等奖并保送重庆南开中学理科竞赛实验班。
高一获得重庆市数学竞赛一等奖,全市第三名。高三获得全国高中数学联赛一等奖,生物联赛二等奖。
7年理论数学的研究和相关教学经验,曾系统教授过大学数学系本科至研究生大部分专业课程。
读博期间曾参与了大量AMC与美国大学生数学竞赛(Putnam、Virginia Tech等)的讲座与培训工作。
辅导战绩:
2023-2024年AMC及AIME战绩(不完全统计):
AMC10、12辅导晋级AIME人数79+,其中前1% DHR20名,最高分满分145.5;AIME 10分+ 学员20名,7分+学员29名。其中14分一人,13分一人,12分六人,11分八人,10分四人。11名学员达到USA/JMO分数线。
2022-2023年AMC及AIME战绩(不完全统计):
AMC10、12辅导晋级AIME人数51+,其中前1% DHR11名,最高分满分150;AIME 10分+ 学员7名,7分+学员11名。其中13分两人,12分一人,11分两人,10分两人。5名学员达到USA/JMO分数线,三名学员分别实际晋级USAMO和USAJMO。
G老师
北京大学硕士毕业
曾获全国大学生数学建模竞赛一等奖;全国高中数学联赛二等奖,全国希望杯数学竞赛三等奖。
辅导战绩:
美国AMC12/10/8竞赛学生进复赛以及获奖率超过65%,AMC12最高分150,140+的不少,AMC10最高分144;比如2022年17个学生晋级AIME,4个拿下1%;2023年二十几个学生晋级AIME,基本都是前5%或1%;欧几里得竞赛学生获奖(前25%)率75%左右,最高分94;澳大利亚AMC竞赛学生也取得了靠前的奖项;
ALEVEL学生A以及A*率96%以上,高数有学生FP1 FM FP2三门离满分差1分;AP微积分学生5分率95%;IB学生提分很快,目前IB HL学生基本都提到7分,SL曾有学生从1-2分提到5-6分用了3个月左右。
AMC辅导课程
课程将涵盖AMC数学竞赛中的常见题型和解题技巧,包括代数、几何、概率等方面,并为学生提供模拟测试和个性化反馈,以强化他们的技能和自信心。课程将为参与者提供全面的指导和支持,帮助他们克服难关,顺利完成AMC数学竞赛的考试。
Pre-AMC8课程大纲
1.Exponents 幂得认识与运算(6H)
a)Squares and Cubes 平方和立方
b)Higher Exponents 高次幂的运算
c)Zero and Negative Exponents 零次幂与负次幂
d)From Squares to Square Roots 平方与平方根
e)Square Roots of Non-square Integers 非平方数的平方根
f)Arithmetic with Square Roots 平方根的运算
2.Number Theory 数论 (4H)
a)Multiples and Divisor 倍数与除数
b)Divisibility 整除
c)Prime Numbers and Prime Factorization 质数与质因数分解
d)LCM and GCF 最大公因数和最小公倍数
3.Fractions 分数 (9H)
a)Multiplying and Dividing by a Fraction 分数的乘除法
b)Raising Fractions to Powers 分数的幂运算
c)Simplest Form of a Fraction 分数化简
d)Comparing Fractions 分数比较大小
e)Adding and Subtracting Fractions 分数加减
f)Mixed Numbers 带分数
g)Percepts 百分数
h)Percent Increase and Decrease增长与降低百分比
i)Word Problems 相关应用题
4.Decimals 小数 (2H)
a)Arithmetic with Decimals 小数运算
b)Rounding 估算与近似
c)Decimals and Fractions 小数与分数的转换
5.Equations and Inequalities 等式与不等式 (4H)
a)Expressions 代数式
b)Solving Linear Equations 一次方程
c)Word Problems 相关应用题
d)Inequalities 不等式
6.Ratios, Conversions, and Rates 比例,转换率与比率 (5H)
a)Ratios 比例
b)Proportions 等价比例(分数)
c)Conversions 转换率
d)Speed 行程问题
e)Other Rates 其他相关的比率问题
7.Angles 角度 (4H)
a)Parallel Lines 平行线
b)Angles in a Triangle 角度与三角形
c)Exterior Angles 外角
d)Angles in Polygons 角度与多边形
8.Triangles 三角形 (9H)
a)Congruence 全等
b)Isosceles and Equilateral Triangles 等腰与等边三角形
c)The Pythagorean Theorem 勾股定理
d)Some Special Triangles 特殊三角形
e)Similar Triangles 相似三角形
f)Perpendicular Bisectors of a Triangle 三角形的垂直平分线
g)Medians and Altitudes 中线与高
9.Quadrilaterals 四边形 (3H)
a)Trapezoids 梯形
b)Parallelograms 平行四边形
c)Rhombi 菱形
d)Rectangles 长方形
e)Squares 正方形
10.Circles 圆 (4H)
a)Arc Measure, Arc Length, and Circumference 弧长与周长
b)Area 面积
c)Funky Areas 特殊部分面积
d)Tangents 相切
11.Three-Dimensional Geometry 立体几何 (2H)
a)Prisms 棱柱
b)Pyramids 锥形
c)Regular Polyhedron 多面体
12.Data and Statistics 数据统计 (2H)
a)Basic Statistics 统计基础
b)Tables, Graphs, and Charts 表格与统计图
c)Sets 集合
13.Counting 计数 (6H)
a)Counting with Addition and Subtraction 加法原理
b)The Multiplication Principle 乘法原理
c)Casework 分类讨论
d)Counting Pairs 计数成对项
e)Probability 概率
1. Number theory
(1)Prime Factorizations
(2)Factors
(3)Base Number and Digits
2. Algebra
(1)Sequences and Series
(2)Special symbols and operations
(3)Ratios, Rates, and Proportions
(4)Functions
(5)Equation Inequations
(6)Sets and Venn Diagram
3. Geometry
(1)Angles and Polygons
(2)Triangles and Pythagorean
(3)Volumes
(4)Circles
4. Probability and Statistic
(1)Statistics
(2)Permutations and Combinations
(3)Probability
(4)Logic and Reasoning
Number theory
Divisor Problems of integers:Exponents, Prime factorization, Number of divisors, LCM and GCD
Remainder Problems of integers:Modulus, Congruence and its properties, simple Modular algebra
Digit Problems in different base representations :Base-10 representation, Base-2 representation, Different base conversion
Divisibility Problems :Divisibility rules; Venn diagram, Sets, *Union formula for two/three sets
Algebra
Sequences:Arithmetic Sequences, Geometric sequences, Simple Repeating Sequence
Algebraic Operations and Polynomials :Expansion and Factorization Formulas; *Binomial theorem, Pascal Triangle; Polynomials, Division Algorithm, Remainder Theorem
Functions and Graphs :Linear Functions, Quadratic Functions, *Rational Functions, Absolute Value Functions
Solving Equations :Linear equations and quadratic equations, Vieta’s theorem for quadratic equations
Geometry
Inequalities and Extreme Value Problems :Linear inequalities and System of linear inequalities; AM-GM inequality, Absolute value inequality
Triangles :Similar and Congruent; Angle bisector and the Angle Bisector Theorem, Median and the Centroid; Pythagorean Theorem, *Heron's formula
Polygons :Trapezoid, Parallelogram, Rhombus, Rectangle, Square
Circles:Chords, Arcs, Angles and Areas; Inscribed Circles and Circumscribed Circles; *Four Concyclic Points
Simple Solid Geometry :Rectangular Box, Prisms, and Pyramids; Sphere and Cones; Lines and Planes in Space
Combinatorics
Counting Problems :Sum rules and Product rules
Permutation Problems and Combination Problems :Permutation Numbers and Combination Numbers; Balls into Boxes Problems
Simple Probability Problems :The Concept of Probability and basic Properties;
Number Theory
Fundamentals :Advanced Complementaries
Prime factorization, Number of divisors, LCM and GCD :Sum/Product of divisors, Euclidean Algorithm and its extensions, Bezout's Theorem
Congruences and Divisibility :Euler’s function and theorem, Fermat’s little theorem, Wilson's Theorem, Chinese remainder theorem(CRT)
Character of digits, Base-n representation:Infinite decimal, Advanced Base-n representation problems
Algebra
Arithmetic and geometric sequences, periodic sequence :Recursive sequence and Characteristic Equation Method
Logarithm:Complicated Logarithmic calculation
Trigonometry:Advanced trigonometry identities
Algebraic Manipulations and Polynomials :Fundamental Theorem of Algebra, Remainder's Theorem, Rational Root Theorem, Generalized Vieta's Theorem
Inequalities and Extreme Value Problems :Fundamental inequalities, Cauchy's inequality, other advanced inequalities
Complex Numbers :DeMoivre' Theorem, Roots of unity, Vector Transformation
Geometry
Basics in Geometry:The law of sines, The Law of Cosines; Heron's formula
Triangles:Centers of triangle, Menelaus's theorem, Ceva's theorem, Stewart Theorem
Circles (chord, angles, area) :Inscribed and circumscribed polygon/circle, Cyclic Quadrilateral, Ptolemy's theorem
Solid Geometry: Theorem of three perpendiculars, Euler's Polyhedron Formula
Combinatorics
Sum rules and product rules:Advanced problems in sum rules and product rules
Permutations and combinations:Advanced problems in combinatorics
Probability and Logic Reasoning :Geometric probability, Recurisve Method, and Pigeon's Hole's Principle
扫码了解课程详情,试听名师课程
领取课程优惠+一对一学术规划!


