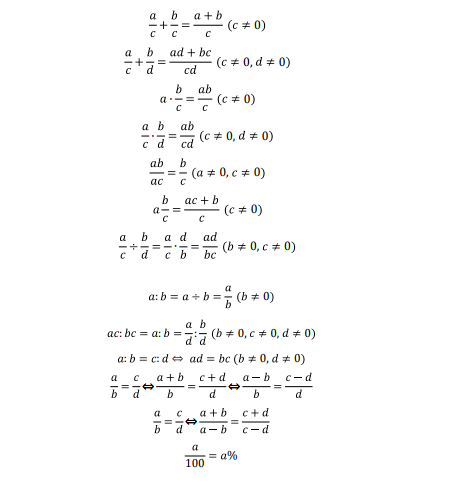随着AMC8在国内认可度的不断增加,越来越多的低年级学生(尤其是4至6年级的学生)开始参与其中。参加AMC8不仅对数学学霸有利,也能极大地帮助普通学生提升数学思维能力。
体制内学生有必要参加AMC8 吗?
1.知识点覆盖:
- 高度吻合:AMC8数学竞赛的知识点大纲与上海体制内6-9年级数学教材内容高度吻合,这意味着学生在备考AMC8时,能够有效巩固校内所学知识。
- 超出范围:AMC8的知识点范围超出了江苏、浙江地区校内数学的知识点范围。通过备考AMC8,学生可以接触到更多、更广泛的数学知识,提升整体数学水平。
2.深度与广度:
- 更高要求:AMC8竞赛的深度和广度高于国内的数学竞赛,要求学生不仅掌握基础知识,还需进行更深入的学习和思考。
- 全面理解:这种学习方式有助于学生对数学知识的全面理解和掌握,培养他们更强的数学思维能力。
3. 择校优势:
对于计划从体制内转到国际学校的学生,AMC8竞赛成绩可以作为加分项,显著提升择校竞争力。
许多国际学校的入学考试题目与AMC8数学竞赛类似,甚至有时会使用AMC8的原题。备考AMC8可以帮助学生适应国际学校的考试模式,增加录取机会。
4.数学思维能力提升
逻辑思维:
AMC8竞赛注重考察学生的逻辑思维能力,通过解决复杂的数学问题,学生可以锻炼自己的逻辑推理能力。这种能力在解决校内数学问题时同样重要。
实际应用:
竞赛题目往往具有实际应用背景,需要学生将数学知识应用于实际问题中。通过AMC8的备考和竞赛,学生可以提升问题解决能力,更好地应对校内数学中的应用题和复杂问题。
参加AMC8数学竞赛对体制内学生来说是非常有必要的。通过备考和参赛,学生不仅能够巩固和拓展校内数学知识,还能提升逻辑思维和问题解决能力。此外,AMC8竞赛成绩在择校和申请国际学校时具有显著的优势,有助于学生在学术道路上取得更好的成绩和发展。
2024年AMC8火热报名中,扫码领取报名表!

扫码免费领取AMC8近20年中英真题+备考教材+AMC8必备公式集+词汇表!